Disjoint Set or Union-Find
Table of Contents
Disjoint Set or Union-Find #
The disjoint set is a data structure that stores a collection of disjoint (non-overlapping) sets. It is initialized with a fixed number of elements and initially each has their own subset. Through calling union(x, y) theses subsets merge together.
Connections follow the transitive property meaning, if A is connected to B, B is connected to C, then A is connected to C.
A common example where this can be used is in Computer Networks. Using a disjoint set we can determine if Computer A and Computer B need to establish a new direct connection or if we can utalize existing connections.
API #
We will use a single array of integers as our base datastructure
- indices = elements of set
- value = set number it belongs to
- The set number doesn’t matter as long as all elements in the same set share the same id.
class UF:
def __init__(self, n):
"""initialize n sets with integer names (0->n-1)"""
self.sets = list(range(n))
self._count = n
def union(self, x, y):
"""add connection between x and y"""
def find(self, z):
"""get root of z"""
def connected(self, x, y) -> bool:
"""return true if x and y have the same root"""
return self.find(x) == self.find(y)
def count(self):
"""number of sets (1 -> n)"""
return self._count
Quick Find #
The find() method is easy to remember to implement. We just return the value at the index of our parameter, quick!
def find(self, z):
"""get root of z"""
return self.sets[z]
For union() it’s a bitt more effort. We iterate over the array and set the root of one of the parameters to the root of the other.
def union(self, x, y):
"""add connection between x and y"""
x_root = self.find(x)
y_root = self.find(y)
if x_root == y_root: return
for i in range(len(self.sets)):
if self.sets[i] == x_root:
self.sets[i] = y_root
self._count -= 1
This results in the following time complexity
| find(z) | union(x, y) |
|---|---|
| O(1) | O(N) |
Quick Union #
Now what if we made the union() method faster? Instead of iteration the array every time we could just set one’s root to the other.
def union(self, x, y):
"""add connection between x and y"""
x_root = self.find(x)
y_root = self.find(y)
if x_root == y_root: return
self.sets[x_root] = y_root
self._count -= 1
But to make this work we have to update how we find the root.
def find(self, z):
"""get root of z"""
while z != self.sets[z]:
z = self.sets[z]
return z
Unfortunatley this makes our overall time complexity slower.
| find(z) | union(x, y) |
|---|---|
| O(N) | O(N) |
Weighted-Quick Union #
If we think of our array as a set of trees, where the value at the index is the root. Then we can see how worst case for Quick Union would result in tree that looks like an array rotated 90 degrees.
So what if we had two sets and wanted to connect them. Which one would be better?
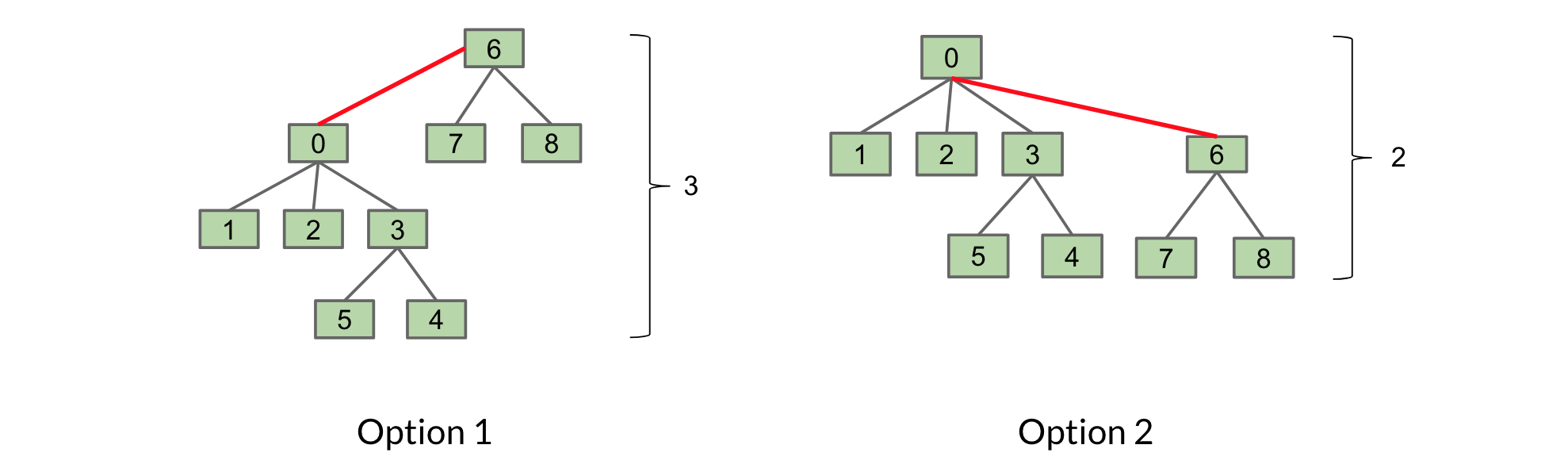
Option two would be optimal and would ensure that the maximum height of any set would be O(log N).
def __init__(self, n):
"""initialize n sets with integer names (0->n-1)"""
self.sets = list(range(n))
self.sz = [1] * n
self._count = n
def union(self, p, q):
i = self.find(p)
j = self.find(q)
if i == j: return
if self.sz[i] < self.sz[j]:
self.sets[i] = j
self.sz[j] += self.sz[i]
else:
self.id[j] = i
self.sz[i] += self.sz[j]
self.size -= 1
| find(z) | union(x, y) |
|---|---|
| O(log N) | O(log N) |
Weighted-Quick Union (with path compression) #
But can we do even better? Well whenever we call find(z) we have to travrese the path from x to the root. So, along the way we can connect all the items we visit to their root at no extra asymptotic cost!
def find(self, x):
if x == self.id[x]: return x
self.id[x] = self.find(self.id[x])
return self.id[x]
This results in the average runtimes to be almost constant. Or calling it the amortized runtime.
| find(z) | union(x, y) |
|---|---|
| O(α(N))* | O(α(N))* |